Derivative pricing and risk management with neural networks

LISTEN TO AUDIO VERSION:

Derivative pricing in financial institutions

Derivatives are complex financial instruments broadly used within financial institutions. As such, their prices are an important information in the different areas of these institutions ranging from relevant pricing information for the front office to calculating their fair value for the financial statements.

Depending on the area, different requirements for the respective pricing models regarding precision, performance and explainability exist.

On the one hand, explainability and precision are of utmost importance for derivative prices within the balance sheet and the regulatory risk management. In other areas, especially due to the high frequency of derivative markets, precision and explainability could be reduced slightly in favor of a high-performance method that can instantly produce pricing indications.

Figure 1: Overview of usage and requirements for derivative pricing

Currently, the main models used for derivative pricing are based on arithmetical models, which excel at precision and explainability. Their weakness, however, is their performance. Especially for more complex options, time-consuming methods like Monte Carlo simulations or stochastic partial differential equations are currently used.

To increase the performance, linearization models such as delta-normal or regression models could be used in theory. However, these models are not very precise due to their nature and hence their use for financial institutions is very limited.

Due to the vast development of machine learning methods within recent years, these new technologies provide the possibility to fill this white spot. Once trained, machine learning models offer a very fast and, as demonstrated in our case study below, relatively precise pricing mechanism.

One of the main takeaways from this case study is that derivative valuation using machine learning may be the future in several areas of financial institutions.

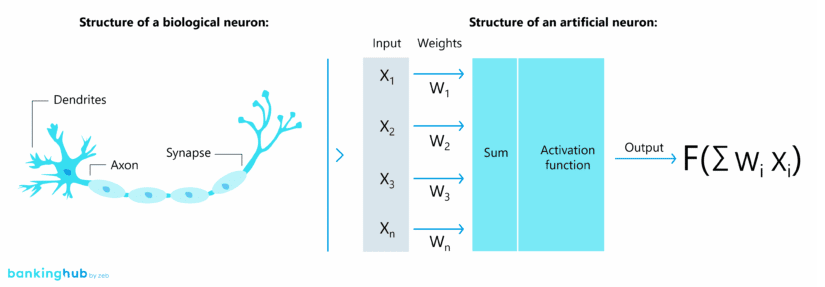
Functioning of a neural network

The artificial neural network is one of the most popular machine learning methods and was hence considered for the derivative pricing use case. This model represents a network of artificial neurons whose operating mode is inspired by the biological brain.

Figure 2: Operating model of a neural network

The reason for choosing a neural network to tackle the issue of derivative pricing is its strength to map very complex relationships of input and output variables without any further information on the relationship. In fact, it has been proven that neural networks can approximate any continuous function under mild assumptions^[1][2]. Similar to several machine learning models, a neural network simply requires a sufficiently large set of training data to calibrate the model and therefore has a wide range of applications including derivative pricing.

Case study: application of the neural network to price American put options

To validate the possibility of using neural networks for the pricing of derivatives, an appropriate derivative was required. The requirements were a sufficient availability of market data to account for the required larger amount of data to train neural networks and a sufficient complexity of the financial instrument itself. Based on these considerations, American options were chosen for the use case.

American options

American options can be exercised at any time within a certain period of time. This is different to European options that can only be exercised at a defined point in time – known as the expiration date. The option to exercise at any point in time massively increases the complexity of pricing. For this reason, the valuation of an American put option cannot be done by means of an analytical formula such as Black-Scholes-Merton. For a successful valuation, stochastic models such as Monte Carlo simulation, binomial models, etc. must be used. As mentioned above, these models are characterized by a very high precision of the results, but take up a lot of computing time. Therefore, a neural network was used to price American put options in this case study to demonstrate the amount of time a neural network can potentially save while maintaining a sufficiently high level of precision when applied to complex derivatives.

Procedure and results

In a first step, a training data set consisting of American options with different maturities (7T – 365T) and moneyness (ATM, OTM and ITM) over a history of three years was created using actual data of options on the S&P100. In addition to information on the exchange-traded price of the option (the targeted output variable), implied volatility based on European options with a similar design, underlying price, maturity, risk-free interest rate and a control variable were also included in the data set. On this basis, the neural network was trained until it delivered robust in-sample results. In the last step, the neural network was applied to an out-of-sample data set and the results were examined in more detail. The out-of-sample data set is located at the end of the data set time horizon to demonstrate the realistic precision of the model when it is only learning from past data.

Figure 3: Operating model of a neural network to price American put options

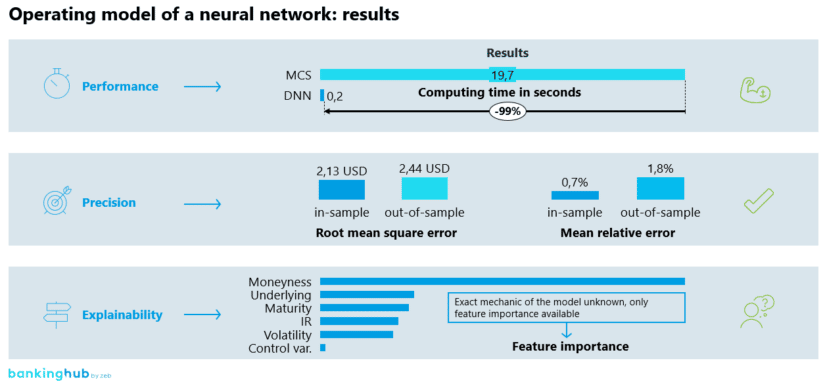
As expected, the impressive feature of the neural network was its short computing time in contrast to conventional stochastic models, especially to Monte Carlo simulation methods. The neural network was able to determine a price for the American option almost instantaneously.

In addition, the neural network was able to approximate the price of American put options at a high precision level. The mean absolute percentage error of the results was 1.8%, which is an excellent estimate of the real price of the option.

One of the main disadvantages of a neural network is its lack of transparency regarding the underlying calculation to derive the results. In order to be able to interpret the results of a neural network, a feature importance can be created which is listing the used variables by their impact on the result. It is visible that the moneyness played a very significant role in the valuation of the option. This can be explained well from an arithmetical point of view, since the moneyness reflects the inherent value of the option and plays an overriding role for in-the-money options. Other important input data in the valuation of the option were the price of the underlying, the maturity, the risk-free interest rate and the implied volatility. The influence of these variables would also be expected from an arithmetical point of view and essentially represents the time value of the option.

It can also be seen that the control variable had almost no effect on the valuation. Summarizing, the feature importance is as it would be expected from an arithmetical perspective, thus confirming the correct functioning of the model. This demonstrates that, even though the model cannot be explained exactly, the quality of the results can be assured to a certain extent.

Conclusion and outlook

Machine learning, especially neural networks, is a very powerful tool applicable in a wide range of scenarios and models, especially for the financial services industry. This case study demonstrates its usefulness in derivative pricing where the neural network model delivers very fast but still robust results. It should also be noted that due to the availability of open-source code libraries, the technical implementation of a neural network is, once a sufficiently big data set of input and output variables is available, surprisingly simple. Beside the collection of the data, the main focus and effort lies on the functional definitions, interpretation of the results and the integration into existing processes.

Due to the mechanics of the neural network which are unknown, the explainability of the results is limited and hence making the model redundant for regulatory or financial reporting tasks. However, for other application areas, especially front office or internal risk management tools, the requirements for explainability are subordinate, hence a neural network could provide essential support, especially due to its very short computing time and high precision.

This use case should be seen as a first step in order to prove the usefulness of neural networks for derivative pricing and risk management. For implementing it in a real scenario within the financial services industry, a deeper analysis with a longer time period and further derivatives would be required.