|
Getting your Trinity Audio player ready...
|
Despite the fact that negative interest rates had already been observed for different tenors over the past months, rates dropped to an unprecedented low as a consequence of the SNB’s decision to change its CHF/EUR policy on January 15, 2015. In fact, after the new policy was implemented in January 22, maturities of up to 10 years were quoted negative. From a strategic point of view, the erosion of deposit margins is among the most crucial challenges. But the negative interest environment also causes a whole array of problems with regard to ALM. In the following, we will focus on its implication for interest rate risk management.
INTRODUCTION OF A SAMPLE CASE FOR THE NEGATIVE INTEREST ENVIRONMENT
In the context of negative interest rates, questions relating to the allocation of negative rates to customers are among the most controversial ones: should customers be charged negative interest rates? Some banks have come to pass negative interests to larger institutional or corporate clients. In the interbank market as well, some banks seem to accept negative interest rates. However, they are not yet willing to take this action unconditionally for retail customers, too. There is too much fear of the ensuing reputational damage. Negative interest rates for savings deposits are off limits for now.
The decision not to allocate negative interests to customers has an influence on the bank’s interest rate risk, as the following example will illustrate. Figure 1 shows the balance sheet of the sample bank. On the asset side, there is a 10-year fixed interest loan, on the liability side the bank has 3-month term deposits. To begin with, it is assumed that the bank operates in a normal interest environment, i.e. a positive curve with a positive slope. The market interest rate for the 10-year maturity period is 2 percent, the rate for 3 months is 1 percent. For the sample bank, margins of 50 and 20 bp respectively are assumed for the sales units as specified in Figure 1.
In addition, for purposes of internal calculation, the bank is assumed to follow the matched maturity approach. The interest rate risk is recognized in ALM, so that the business units are left risk free with respect to interest rate risk. For ALM, the risk becomes evident as a maturity gap in the gap analysis report as shown in Figure 2.
The risk results from the maturity incongruence in the fixed rate periods of assets and liabilities, in particular the difference between a 10-year asset maturity and a 3-month liabilities maturity. In the example, assume that this risk is perfectly hedged by means of a payer swap to 3 month. With respect to the current interest rate curve, the spread amounts to 100 basis points (10-year 2% minus 3-month 1%).
With the interest rate risk hedged, interest changes do not have a P&L influence anymore. This holds true on bank level but also on segment level, i.e. Lending, Deposits and ALM. Any changes to the 3M Libor are balanced out between payer swap and the 3m term deposit client rate. Thus, the interest rate change is irrelevant for the asset side by definition; the ALM interest income is hedged; and the deposit business earns a constant margin by adjusting the client rates according to the 3M Libor.
INTERNAL EFFECT ON RESULTS IF INTEREST RATES FOR CUSTOMERS ARE NOT ADJUSTED
Now, assume the 3M Libor turns negative and the bank decides not to pass this on to the customer. The client rate for deposits is set to zero. What is the impact on the segment’s interest income and risk? As before, the lending business would not be affected by the interest rate change. However, in order to understand the effect on the interest income for the deposit business, an internal allocation rule must be decided on.
For this, there are two possible options: First, ALM can pass the negative 3M Libor on to the deposit business as it did before. This way, the interest income of ALM would be unaffected by the change in interest rate. However, the deposit business is left with a lower margin now, because the units have to pay the (now negative!) interest rate to ALM through the internal allocation mechanism, but, at the same time, cannot pass this negative rate to the client. Thereby, the unit loses part or all of their initial margin of 20 basis points. They even might end up with a negative margin. In contrast to the initial assumption, the deposit business would not be protected against the interest rate risk. This is in contradiction to the matched maturity method, where the business units transfer interest rate risks to ALM.
A second possible internal cost allocation rule would be that ALM guarantees the originally planned margin of 20 basis points to the deposit business. This way, the interest income of the deposit business remains unaffected by negative interest rates. But now, the costs would be incurred by ALM. This holds true since ALM pays the (negative) 3M Libor through the payer swap and receives a spread of 100 basis points. Since the (now negative) 3M Libor cannot be passed on to the deposit business anymore, a negative interest income effect results for ALM. As a consequence, despite the fact that ALM had initially hedged the interest rate risk by means of the payer swap, the hedge turns out to be ineffective.
The above considerations can be summarized as follows: When not charging clients for negative interest rates, (1) irrespective of the internal allocation scheme, the bank is affected by interest losses; (2) when allocating the interest loss to the business units they would no longer be free of interest rate risks; and (3) the initial interest rate risk hedge looses effectiveness. The interest rate risk of the bank is not—or at least not sufficiently—hedged anymore.
IMPACT OF A LACKING ADJUSTMENT OF THE CUSTOMER INTEREST RATE ON THE ALM STRATEGY
The root of the problems described above results from an implicit interest rate option that is sold to the client when promising non-negative interest rates. In particular, this implicit interest hedge option can be understood as a floor option for which the bank has taken a short position. The bank has sold a floor option to the customer that it is not going to lower the customer interest rate below a zero level.
As it turns out, in the past customers were not charged for the value of such an implicit option, nor was it considered in the internal funds transfer pricing mechanism. However, if the business units should be kept free of interest rate risks, these options ought to be priced and allocated based on market conditions. In addition to the cost allocation scheme, it is also necessary to adjust the instruments for the management of interest rate risk in ALM. Otherwise, the bank would not be able to manage this risk effectively.
The above example clearly shows that a “naive” gap analysis report—which simply states the asset and liabilities positions—does not reflect the actual interest rate risk correctly. An effective interest risk hedging strategy cannot be built on this foundation, because the implicit option would have to be considered in the deposit business.[1] For this end, the gap analysis report could be adjusted in a way that makes the impact of the implicit option on customer funds more evident. What would this look like with regard to the above example?
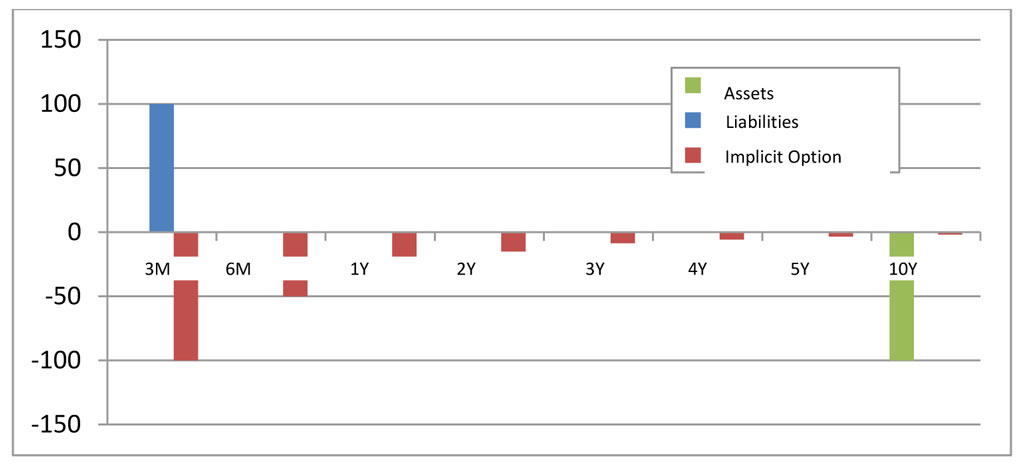
As we have seen, the interest adjustment behavior of customer funds is not described correctly by the 3M Libor anymore. In the case of a guarantee for non-negative client rates, the liabilities side of the sample bank actually corresponds to a portfolio consisting of a short position of 100 at the 3M Libor and a short position of 100 on a floor option at the 3M Libor with a zero floor. In order to simplify the analysis, it is furthermore assumed that the floor position has a maturity of 10 years, i.e. over the next 10 years, the 3M Libor is limited to a minimum value of zero for the customer. In the gap analysis report, the option could be represented through its delta equivalent.[2] This results in the extended gap analysis report as presented in Figure 3.
The figure clearly shows that the floor option leads to an interest rate risk profile that differs from the one obtained from a mere consideration of the two balance sheet positions. In particular, the interest rate risk on the liabilities side is reduced, because the combination of the customer deposit and the short position on a floor option which is sufficiently deep in the money neutralizes its interest rate risk. The sample bank has swapped the 10-year fixed rate to the 3M Libor through a payer swap and as a result, it now lacks the offset through an adjustment of the client rate for the term deposits. Changes to the 3M Libor remain in the bank. The initial hedge through the payer swap is no longer effective. The effect of the floor option continues over time, although in a weaker form.[3] In sum, the risk profile differs from the profile that was assumed when setting up the hedge. Even worse, it can be shown (not formally derived here) that —in the given case— there is no perfect hedge strategy using standard interest swaps only. Under such circumstances, a bank would have to resort to alternative hedging instruments (e.g. futures).
CONCLUSION
In sum, it can be said that (1) the funds transfer pricing mechanism has to take into account existing implicit interest options if business units are to be kept free of interest rate risks; (2) the implicit options also have to be carefully considered for interest rate risk management, including the ALM strategy; and (3) hedging through standard interest swaps becomes ineffective in the current interest rate environment with negative interest rates.




One response to “Negative interest rates in Switzerland – effects on ALM”
Doug
Great note guys…this is giving me a great perspective in any curly questions before the CFA3 exam tomorrow!